Tuning
Tuning is the process by which we choose precisely the frequencies of the Notes we are going to use.
The choice is made taking as a reference the proportions that exist between the frequencies that originate any harmonic sound. These proportions are the octave and the fifth, and are the foundation of the series of natural harmonics upon which all tuning systems and the theory of musical harmony have been built.
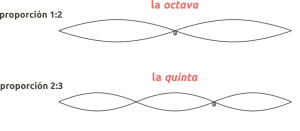
The octave is the relationship between two notes whose frequencies maintain a 1:2 ratio, that is, if we start from a sound with a certain frequency and double its frequency, we can find a second sound that will have twice the frequency and therefore will be an octave away. Due to the great resonance and similarity that exists between two notes that maintain the octave ratio, they are considered two notes of the same type and therefore a way of completing a sound cycle or register.
The fifth is the relationship between two notes that maintain a 2:3 ratio. Thus, we must apply the fifth ratio to generate different notes.
From these two intervals we can generate collections of notes, which although different from each other, maintain a harmonic proportion between them.
At Nuzic we use the equal temperament system(12-TET), and today it is the most widely used tuning system. It divides the octave into 12 equal parts, thus generating the collection of chromatic notes:

In the sound dimension of the Nuzic system, this collection of chromatic notes is organized in 7 registers of 12 notes each, containing a total range of 84 notes.

Although it is most common to divide the octave in twelve equal parts (12-TET), the equal temperament system is very practical and versatile, and it also allows us to explore other sonorities by dividing the octave into any other number of equal parts, for example into 8, 10, 14, 19, 24, 31… For example when we divide the octave in 24 equal parts (24-TET), we expand our initial collection of 84 chromatic notes and obtain the collection of microtonal notes. This expands our total range of available notes to double, making room for quarter tones:
There is no tuning system that establishes perfect harmony. All have their advantages and disadvantages. For this reason, a multitude of systems have been built throughout history that have served some purposes better than others.
We can classify all existing tuning systems into three categories:
- Regular systems
These systems order all their notes from a series of equal fifths, without forming a closed cycle or register (there is a slight decompensation in the successive octaves).
The Pythagorean tuning system (fifths maintain the ratio 3:2), and the mesotonic temperament ( fifths are smaller) belong to this group.
- Regular cyclic systems
They are regular systems that form a closed cycle or register. These systems divide the octave into equal parts.
The equal temperament tuning system (TET) that we have seen above belongs to this group, being one of the most used at present.
- Irregular systems
These systems are formed from fifths of different sizes. Much of baroque music uses this type of temperament.
The best known tuning system of this group is that of just tuning, based on the series of natural harmonics, which define the just intervals between notes. These distances can be expressed by simple fractions.
The temperaments of Kellner, Neidhardt and Werckmeister also belong to this group.


