Cómo calcular la longitud o el ratio de un ciclo polirrítmico
A continuación explicamos qué es la fracción resultante de la voz, y cómo realizar dos cálculos que resultan muy útiles para componer o analizar polirritmias cíclicas.
LA FRACCIÓN RESULTANTE DE LA VOZ
Al combinar los dos elementos que definen cada voz rítmica (la fracción y el iT fijo) obtenemos una fracción resultante (frR). Ésta es la fracción que vamos a usar para calcular tanto la longitud del ciclo polirrítmico como el ratio entre las voces.
![]()
Obtenemos la fracción resultante multiplicando el numerador y el iT fijo de la misma voz (es decir, los dos valores que agrupan pulsaciones), y manteniendo el denominador tal cual. Es importante reducir la fracción resultante a sus valores mínimos cuando sea posible. Veamos un ejemplo:
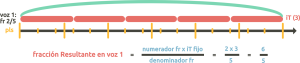
El numerador de la fracción resultante se obtiene multiplicando 2 (numerador de la fracción de la voz 1) por 3 (el iT fijo), dando como resultado 6. Como el denominador se mantiene igual, la fracción resultante es 6/5. En este caso, la fracción no puede reducirse más.
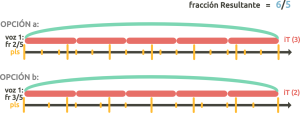
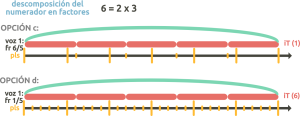
También podemos realizar el proceso inverso: ¿Dada una fracción resultante, cómo expresarla con distintas fracciones e iT fijos? Para calcular las distintas posibilidades, únicamente hemos de descomponer el numerador en sus distintos factores, e ir combinándolos entre el numerador y el iT fijo (el denominador siempre será el mismo). Siempre que sea posible se ha de reducir la fracción final. En la sección de referentes de este nodo puedes usar la calculadora para descomponer cualquier número en factores.
Veamos un ejemplo:
 |
 |
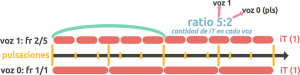
En las polirritmias a dos voces, la longitud del ciclo polirrítmico es la cantidad de pulsaciones que hay entre el inicio del ciclo donde las voces están juntas, hasta el final del ciclo donde las voces vuelven a coincidir, y equivale al numerador de la fracción resultante de la voz 1.
![]()
Veamos un ejemplo:

En este caso la longitud del ciclo polirrítmico es de 6 pulsaciones dado que la fracción resultante es 6/5.
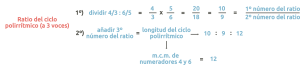
En las polirritmias a tres voces, la longitud del ciclo polirrítmico es la cantidad de pulsaciones que hay entre el inicio del ciclo donde todas las voces están juntas, hasta el final del ciclo donde todas las voces vuelven a coincidir, y equivale al mínimo común múltiplo (m.c.m.) de los numeradores de las fracciones resultantes de las voces.
En la sección de referentes de este nodo puedes usar la calculadora para obtener el mínimo común múltiplo.
Veamos un ejemplo:

En este caso la longitud del ciclo polirrítmico es de 12 pulsaciones (equivale al m.c.m. de los numeradores 4 y 6).