Cómo construir una polirritmia cíclica a partir de un parámetro

¿Qué tipos de parámetros podemos usar para construir una polirritmia cíclica?

Podemos construir una polirritmia cíclica a partir de uno de los siguientes parámetros:

 

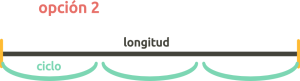
el ciclo debe ser igual a la longitud dada	el ciclo debe estar contenido y sincronizado con la longitud dada	ratio dado

 

• la longitud del ciclo
• la longitud de una sucesión, segmento o idea
• el ratio del ciclo polirrítmico

 

---

1. Construir a partir de una longitud de ciclo
2. Construir a partir de la longitud de una sucesión, segmento o idea
3. Construir a partir de un ratio 

---

 

CONSTRUIR A PARTIR DE UNA LONGITUD DE CICLO

Antes hemos visto cómo calcular la longitud del ciclo polirrítmico a partir de voces rítmicas dadas, definidas con fracciones e iT fijos. También se puede hacer el proceso inverso: partiendo de una longitud de ciclo, podemos calcular todas las posibles polirritmias cíclicas que coinciden con esta longitud.

Cuando se trata de una polirritmia a dos voces, el numerador de la fracción resultante de la voz 1 deberá ser igual a la longitud del ciclo. Para que esto ocurra, tenemos dos opciones (en ambas, cualquier denominador es posible):

1. Partir de una fracción con numerador igual a la longitud y usar un iT (1). (Recuerda que en la app de Nuzic sólo es posible utilizar numeradores de una sola cifra)
2. Escoger un numerador y un iT fijo cuyos valores multiplicados equivalgan a la longitud.

Utiliza la calculadora de factores en los referentes del lateral, para encontrar todas las opciones posibles. Veamos los siguientes ejemplos:

 

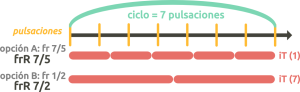(En la app de Nuzic no podemos realizar la opción A, ya que no se permiten numeradores de más de una cifra)

 

Cuando se trata de una polirritmia a tres voces, el mínimo común múltiplo de los numeradores de la frR de la voz 1 y la voz 2 debe ser igual a la longitud. Aquí también tenemos dos opciones. En ambas, cualquier denominador es posible:

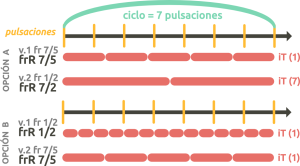
1. Partir de dos FrR cuyos numeradores sean igual a la longitud.
2. Partir de dos FrR con numeradores distintos cuyo mínimo común múltiplo equivalga a la longitud.

Veamos los siguientes ejemplos:

 

 

CONSTRUIR A PARTIR DE UNA LONGITUD DE SEGMENTO, SUCESIÓN O IDEA

Aquí también partimos de una longitud determinada (de una sucesión, segmento o idea), y queremos calcular todas las posibles polirritmias cíclicas que podríamos encajar dentro. Es un proceso parecido al apartado anterior, pero con más posibilidades ya que podemos repetir una o más veces el ciclo polirrítmico, con la única condición de que el final del último ciclo se sincronice con el final de la sucesión, segmento o idea. Así evitamos que el ciclo quede interrumpido (daría error en la app).

Para realizar este cálculo, seguimos los siguientes pasos, tanto si se trata de una polirritmia a dos o a tres voces:

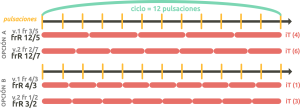
1. Descomponemos en factores primos el número de la longitud dada (utiliza la calculadora en los referentes del lateral)  → Ej: longitud 12 = 2x2x3.
2. Calculamos todas las opciones resultantes de multiplicar los factores entre sí e incluimos el número 1 → Ej anterior: 1, 2, 3, 4, 6 y 12.
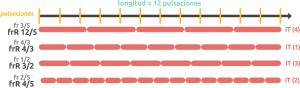
3. Definimos los numeradores de las frR de la voz o voces usando cualquiera de las cifras obtenidas en el paso dos (cualquier denominador es posible) → Ej anterior: posibles frR de las voces en una longitud de 12 pls → frR 12/5, 4/3, 3/2, 4/5, etc…

 

 

CONSTRUIR A PARTIR DE UN RATIO

También hemos visto cómo obtener el ratio de un ciclo polirrítmico a partir de las fracciones e iT fijos de las voces rítmicas. Aquí el proceso inverso consistiría en partir de un ratio y ver qué polirritmias podríamos construir con ese ratio.

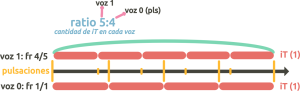
En las polirritmias a 2 voces tenemos una única opción: en la fracción resultante de la voz 1 usarás el 2º número del ratio como numerador, y el 1º como denominador. / Ej: ratio 5:4 → frR voz 1 = 4/5

 

 

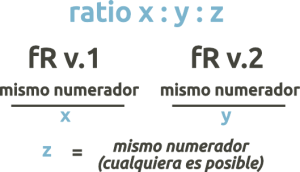
En las polirritmias a 3 voces tenemos distintas opciones con sus variantes:

1. Ratio en los denominadores, mismo numerador
   • Variante: multiplicación de los números del ratio por el mismo número
2. Ratio en los numeradores, mismo denominador
   • Variante: multiplicación de los números del ratio por el mismo número
3. Factorización de los números del ratio, y distribución entre numeradores y denominadores

A continuación profundizaremos en cada opción:

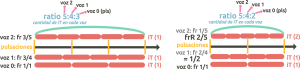
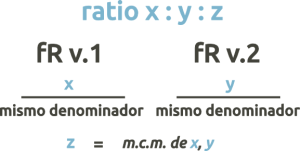
• Los números del ratio se colocan en los denominadores de las voces 1 y 2. Ambas fracciones tienen el mismo numerador (puede ser cualquier número), y se reducen las frR si es posible.

 

 

Veamos con el ratio 5:4 el siguiente ejemplo:

 

 

• • Una variante del caso anterior: los números del ratio de los denominadores pueden estar multiplicados por el mismo número. Cuando el ratio relaciona únicamente las voces 1 y 2, crea un ciclo secundario. Veamos el siguiente ejemplo con el ratio 3:2, donde multiplicamos x2 los denominadores de las fracciones iniciales 5/3 y 5/2: 
    

 

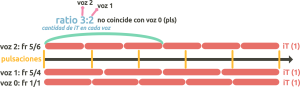
 frR 5/6 y 5/4 → denominadores x2 ; (también podría ser frR 5/9 y 5/6 → denominadores x3, etc.)

 

• Los números del ratio se colocan en los numeradores de las voces 1 y 2. Ambas fracciones tienen el mismo denominador (puede ser cualquier número), y se reducen las frR si es posible. Cuando el ratio relaciona únicamente las voces 1 y 2, crea un ciclo secundario.

 

 

Veamos con el ratio 2:3 el siguiente ejemplo:

 

 

• • Una variante del caso anterior: los números del ratio de los numeradores pueden estar multiplicados por el mismo número. Recuerda que cuando el ratio relaciona únicamente las voces 1 y 2, crea un ciclo secundario. Veamos el siguiente ejemplo con el ratio 2:3, donde multiplicamos x2 los numeradores de las fracciones iniciales 2/5 y 3/5:

 

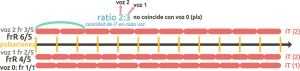
 frR 5/6 y 5/4 → numeradores x2 ; (también podría ser frR 6/5 y 9/5 → denominadores x3, etc.)

 

• Cuando los números del ratio pueden descomponerse en factores primos, podemos distribuirlos entre los numeradores y denominadores de las fracciones de las voces 1 y 2:

 

 

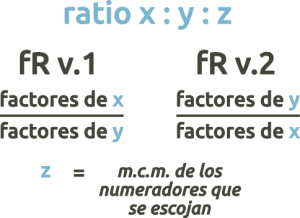
La longitud del ciclo dependerá de cómo distribuyas los números en los numeradores. Puedes utilizar la calculadora de factorización primaria en los referentes del lateral, para descomponer los números del ratio en factores primos. Veamos el siguiente ejemplo con el ratio 21:20:

 

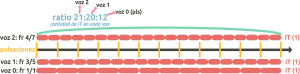
Descomposición en factores primos: 21=3×7 y 20=5x2x2 → frR v.1 = 3/5, y frR v.2 = 4/7 (longitud del ciclo = m.c.m. de numeradores = 12 pulsaciones)