Sets of elements
 |
A set is a grouping of elements of the same type, which facilitates the understanding and organization of any information. Sets have their own identity, which depends on the type of element used and its numerical values.
In the same way that the same person relates in different ways depending on who is in front of them, the same element that relates within different sets, takes on a different meaning in each case. |
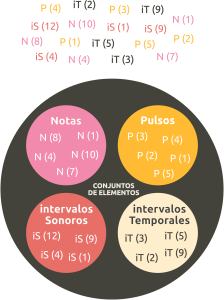
We distinguish 2 types of element sets:
Example of collection: N [0 4 7] Scales, chords or triads are examples of collections, frequently used in music. |
 |
 |
To use a collection and generate a sequence, we choose the elements we are interested in and specify their order, being able to repeat the same element as many times as we want. In this way we generate a succession, starting from a previous collection. |
Example of succession: N (3 5 4 4 8 3 6 4) Rhythmic patterns and rhythmic cells are examples of successions frequently used in music. From a sequence, we can also extract the collection of elements used, which we usually order in ascending order. Example: from the sequence N (3 5 4 8 3 6 4), we extract the collection N [3 4 5 6 8] [3 4 5 6 8] |
Example of succession: N (4 7 7 0 4)
Example of succession: iT (3 3 4 4 2 4) |
COMPLEX ELEMENTS
For example, in a succession of triads, the complex elements are the triads, since each one is a set of 3 Notes by itself. |
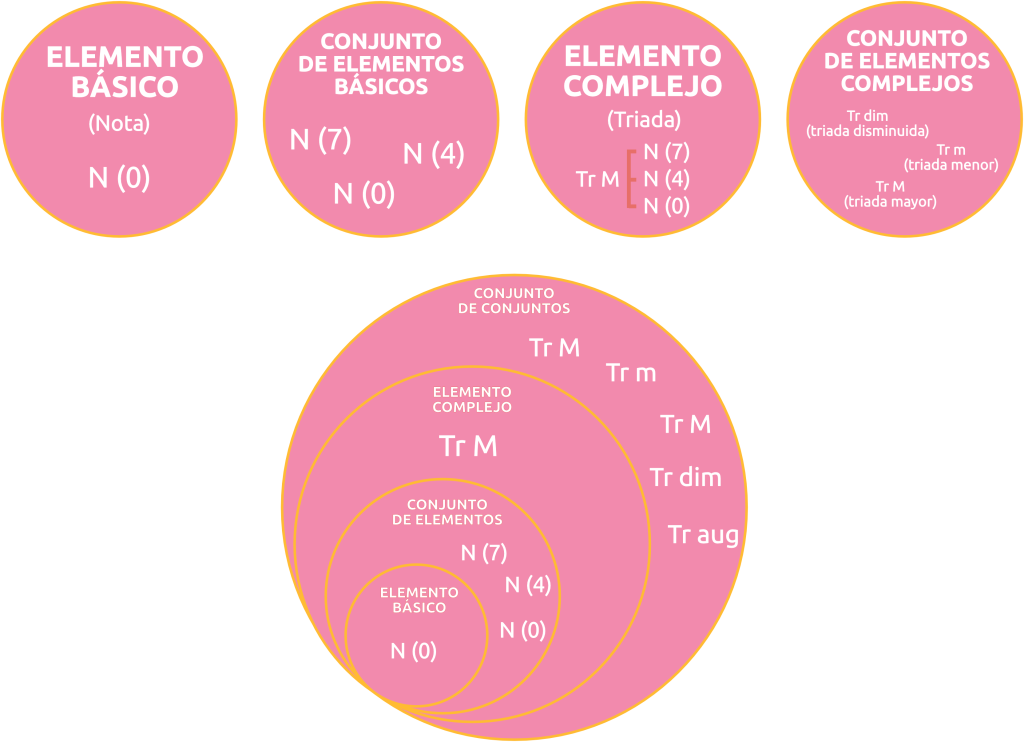 |
Let us now see what set of set possibilities we have:
-
- collection of collections → example: «I want to use these scales in the piece, although I don’t know their order yet».
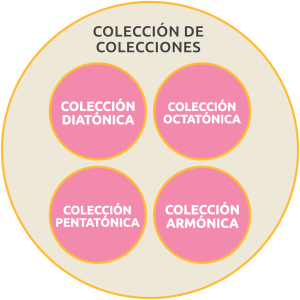
-
-
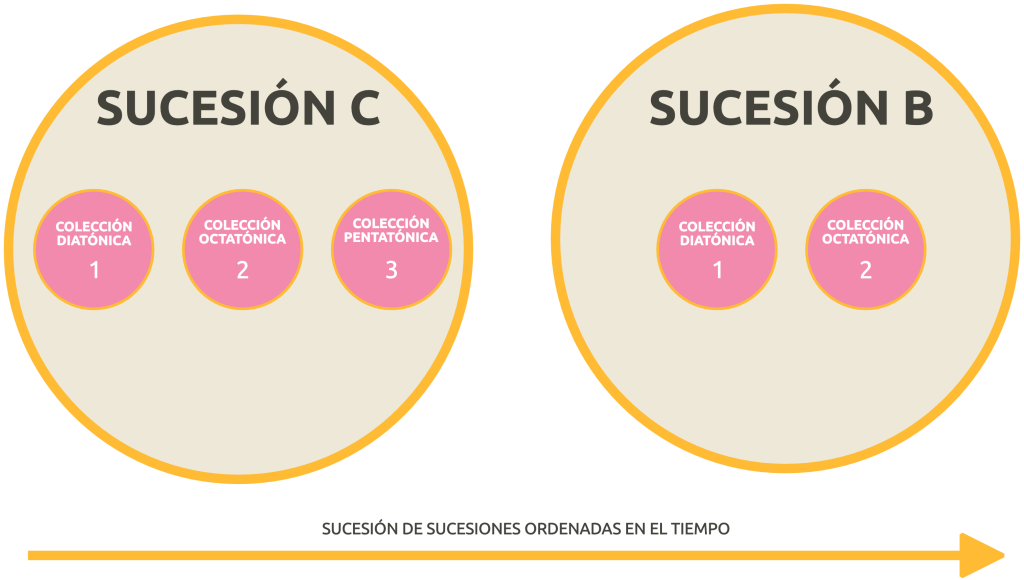
- succession of collections → example: «I want to use these scales in this order».
-

-
-
- succession collection → example: «I create successions, for example of time intervals (iT), but I don’t order them yet».
-
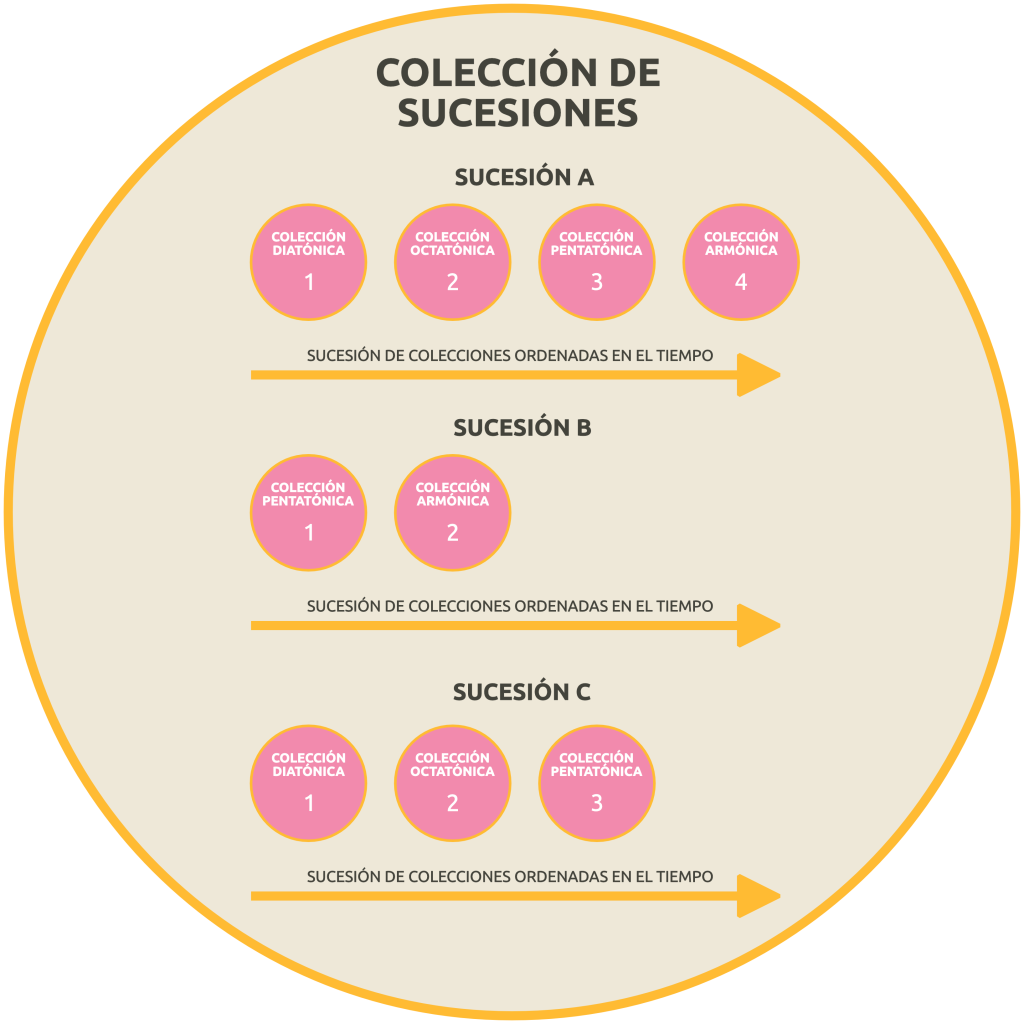
-
-
- The succession of successions → example: «I create successions, and give them an order».
-